Retelling a Proof of Pythagoras's Theorem

I think that a beautiful Maths proof, like a folk tale, should be told and retold.

In this post, I’ll be retelling a simple proof for Pythagoras’s Theorem $a^{2}+b^{2}=c^{2}$ , first shown to me by my Maths Professor Burkard Polster of Mathologer fame.

Even though most of us remember Pythagoras’s Theorem (even vaguely) from high school, typically we never have the opportunity to work through a proof for it. It’s such a shame because of how interesting and simple it can be.

I’d be remiss if I didn’t briefly mention that this is far, far from the only proof for Pythagoras’s Theorem. In fact, Pythagorean Theorem proofs have a long and interesting history in and of themselves, with hundreds of published proofs and many books discussing just them.

For anyone who hasn’t seen this before, I hope this is an easy insight into the elegant and mind shifting world of Pure Mathematics and Maths Proofs. If this is your bread and butter, I hope you enjoy the retelling with me, and please let me know if I did it justice!

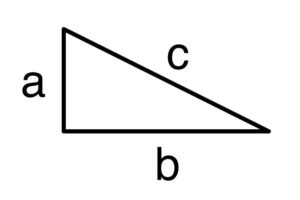
Which one’s Pythagoras’s Theorem Again?

So that we’re all on the same page, Pythagoras’s Theorem is the relationship:

$a^{2} + b^{2} = c^{2}$

Where $a$ , $b$ and $c$ are lengths of a right angle triangle. $a$ and $b$ are the shorter sides and $c$ is the hypotenuse, the longest side.

As well as having deeper mathematical consequences, Pythagoras’s Theorem allows us to easily calculate the length of any side of a right angle triangle, when we know the length of the other two sides.

Proof for Pythagoras’s Theorem

Step 1: Define our Right Angle Triangle

To begin our proof, we start with a right angle triangle of side lengths $a$ , $b$ and $c$ . $c$ is the hypotenuse, the longest side.

Figure 1: The Right Angle Triangle we have defined for this proof

Note: We haven’t actually defined the lengths of any of these sides. This is intentional and will be important at the end of our proof.

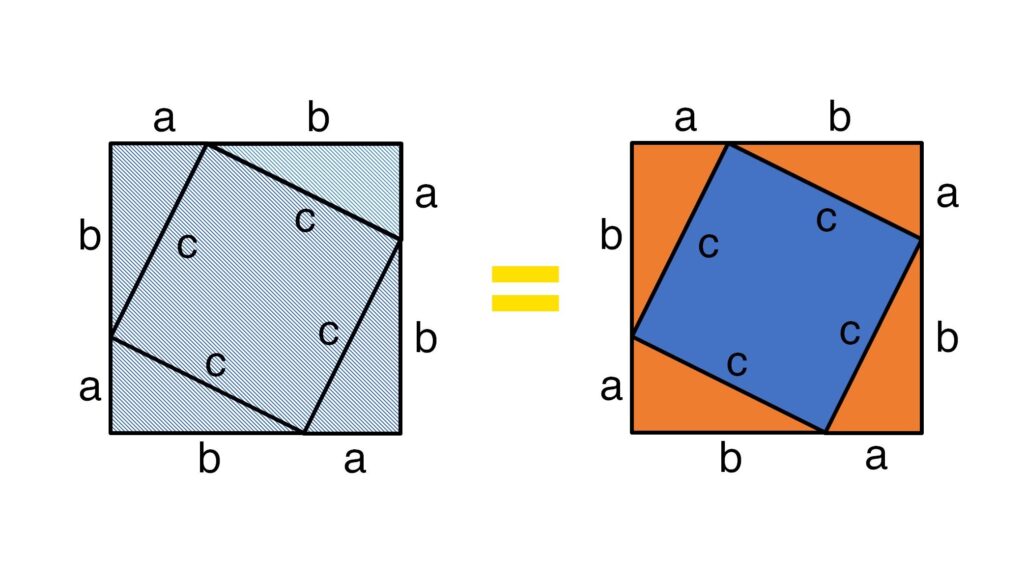
Step 2: Arrange 4 of Our Right Angle Triangles as Follows

We take 4 copies of our Right Angle Triangle and arrange them in the slightly funny shape bellow. Going forward I’ll call this the 4 Triangle Arrangement.

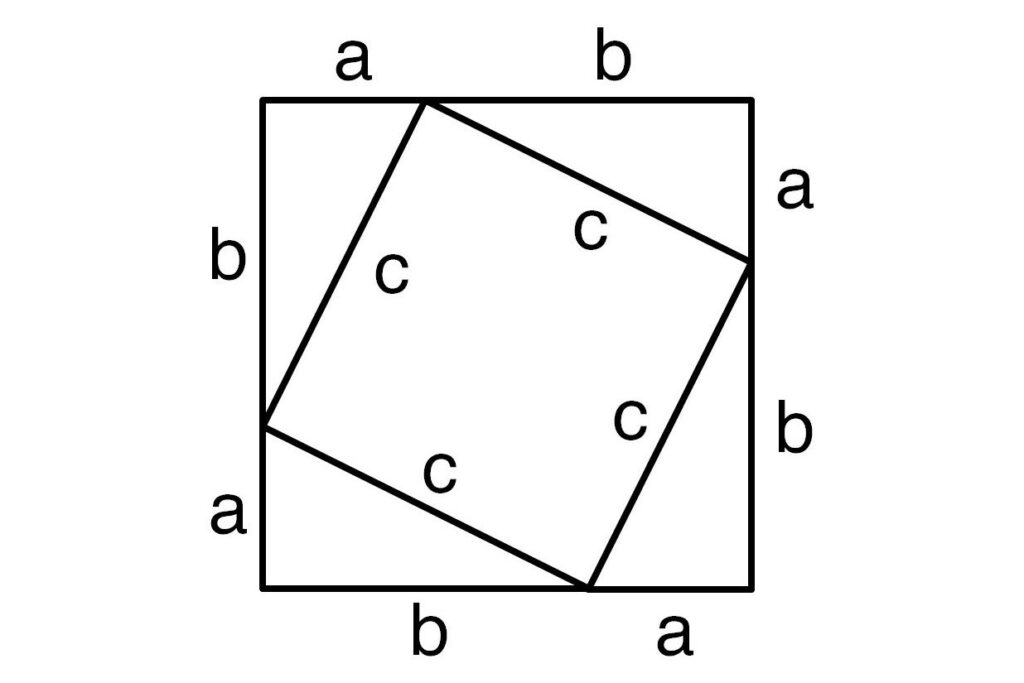
This step is the great insight of the proof. It won’t be immediately obvious why we do this, but I hope that over the next few steps you’ll join me for a eureka moment, where it all makes sense.

Now consider for a moment, how would you calculate the area of our 4 Triangle Arrangement?

Step 3: First Method to Calculate Area, One Big Square

One way to calculate the area of our 4 Triangle Arrangement is to look at it as one large square.

Figure 3: The 4 Triangle Arrangement considered as one large square of side length a+b

As we know, to find the area of a square, we times its side length by itself. In this case, the side length is equal to $a + b$ (as you see from in figure 3), therefore:

$\mbox{Total Area } = (a+b)(a+b)$

Expanding this out

(1) $\begin{equation*} \mbox{Total Area } = a^{2} + 2ab + b^2 \end{equation*}$

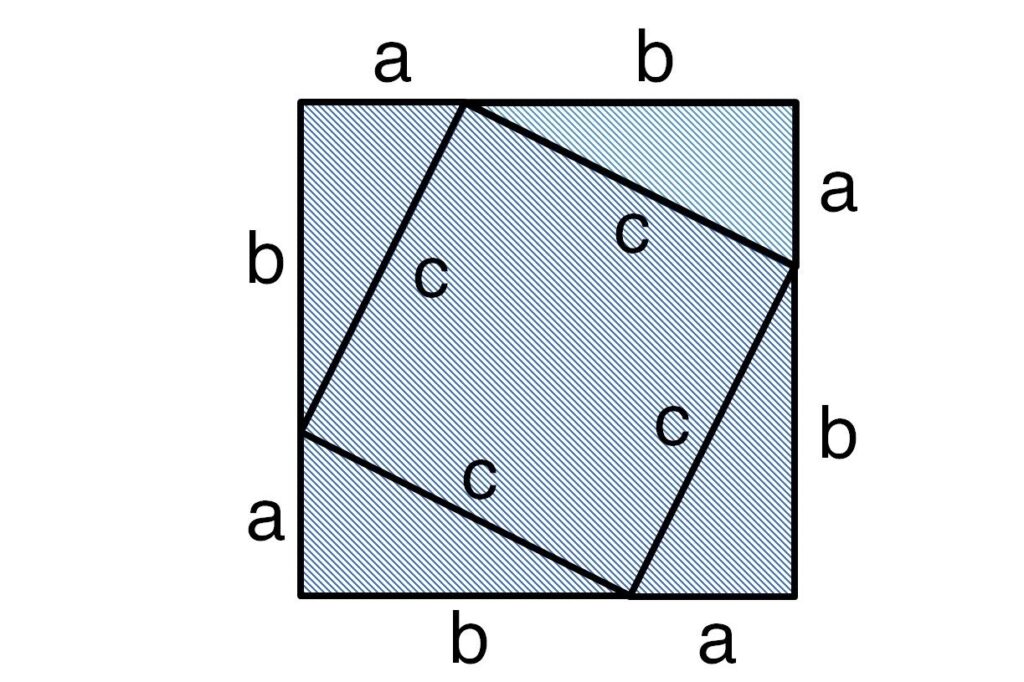
Step 4: Second Method to Calculate Area, 5 Smaller Shapes

Looking at our 4 Triangle Arrangement again, we can also think of it as 4 triangles around the edge plus the square in the middle.

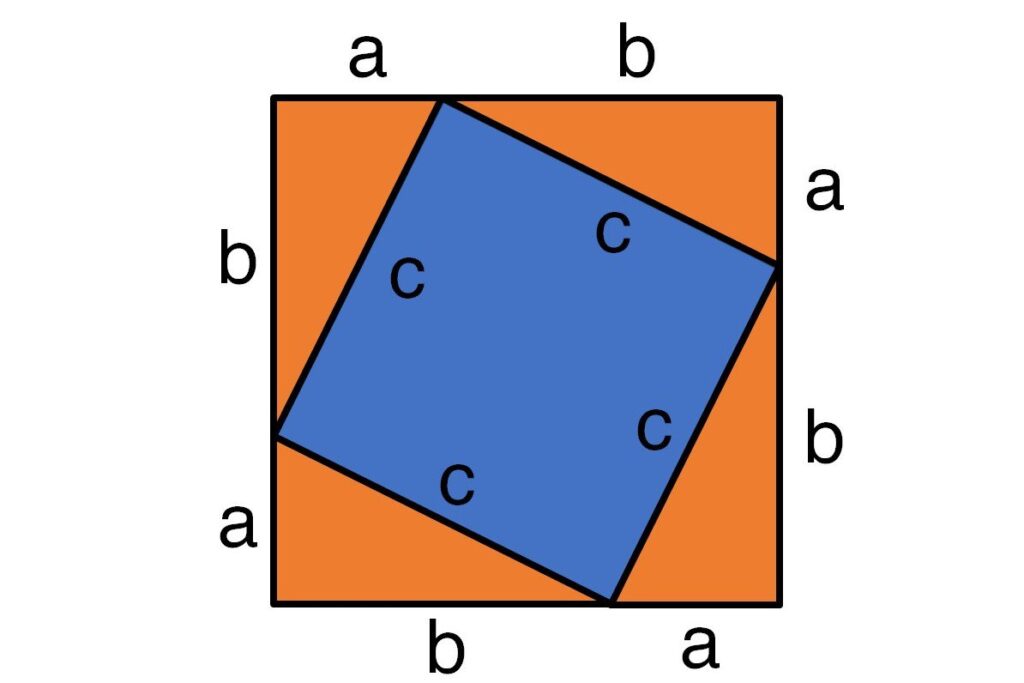
Figure 4: The 4 Triangle Arrangement broken into its 5 smaller shapes

With this in mind, we can work out the total area of the 4 Triangle Arrangement by adding the area of each of these 5 shapes (the 4 outer triangles plus the square in the middle):

$\mbox{Area of the 4 Triangles } = 4 ( \frac{1}{2} a b )$

Rearranging

$\mbox{Area of the 4 Triangles } = 2 a b$

$\mbox{Area of the Square } = c^{2}$

Adding these together we get

(2) $\begin{equation*} \mbox{Total Area } = 2 a b + c^{2} \end{equation*}$

Step 5: Equating Our Two Calculations for Area

In Steps 3 and 4, we calculated the area of the 4 Triangle Arrangement in two different ways, equations $(1)$ and $(2)$ . But clearly these areas are equal, therefore equations $(1)$ and $(2)$ must be equal.

Figure 5: Our Two Methods for calculating the Area of the 4 Triangle Arrangement must be equal

For the final step of the proof we equate $(1)$ and $(2)$ as follows:

$(1)=(2)$

$a^{2} + 2ab + b^2 = 2ab + c^{2}$

Rearranging

$a^{2}+b^{2}=c^{2}$

But isn’t that Pythagoras’s Theorem?

Absolutely! But what does that mean?

Step 6: But what does that mean?

Think back to Step 1 where we defined $a$ , $b$ and $c$ . These are the sides of a right angle triangle, but importantly we never defined their lengths.

This means that we have shown, through the steps we just worked through, that for any right angle triangle the relationship holds:

$a^{2}+b^{2}=c^{2}$

Or put even more simply, we have proven Pythagoras’s Theorem!

And now for the best part, with our work done we get to draw one of these.

❒

That box means QED, or the proof is complete.

Closing Thoughts

Thanks for joining me on this journey. I was excited to try something new with this post and I’m really happy with how it’s turned out. I hope that was even a little bit as fun to read as it was to write.

As always if you have any comments or questions I’d love to hear from you, please get in touch!